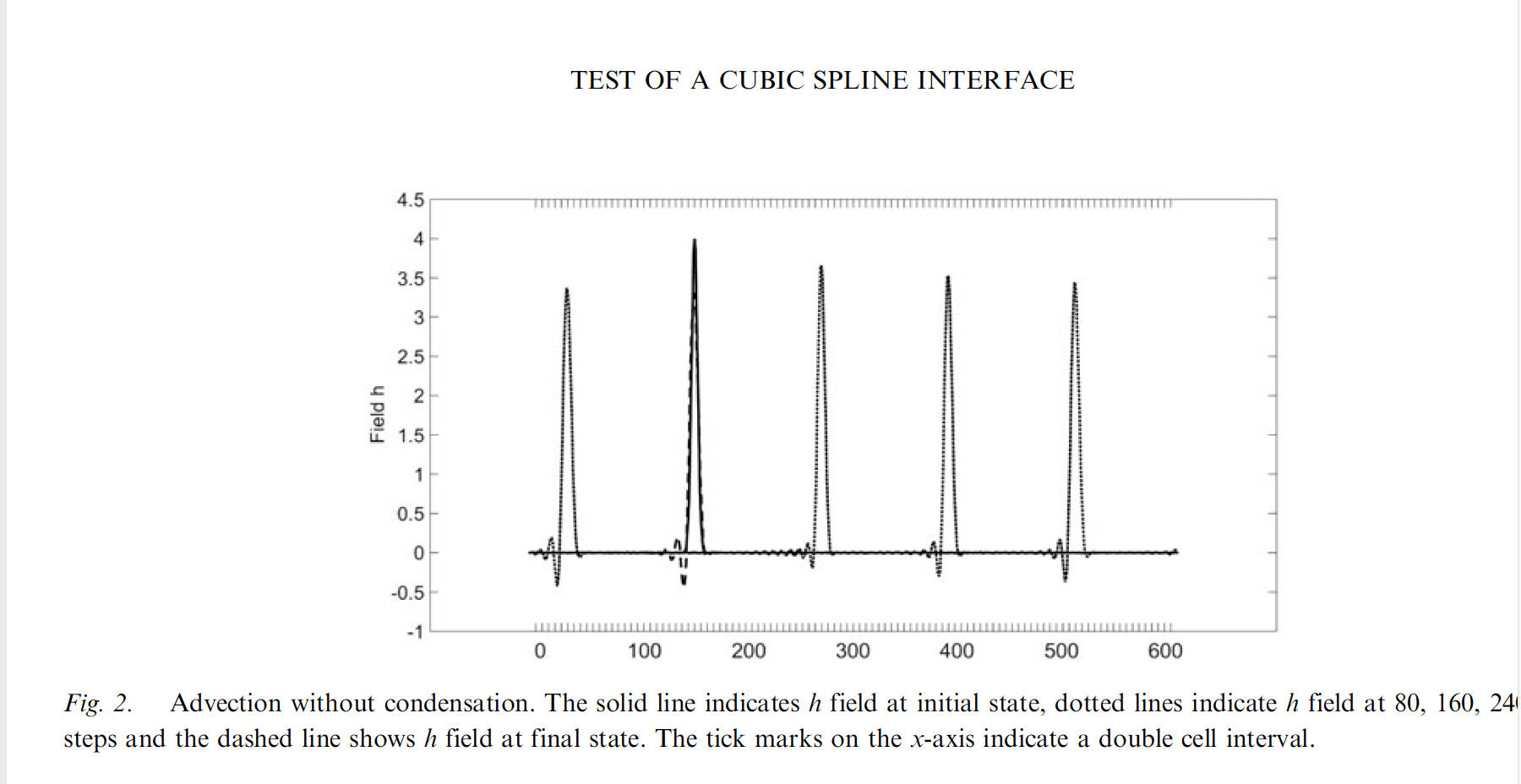
Numerical models of the atmosphere use meshes to describe fields like density to temperature. In the most simple case the mesh is one dimensional and has grid points x_i. A density field h(x) is represented in the simplest case by grid point values h_i = h(x_i). A very simple test case is the the transport of a density field in a homogeneous velocity field, where for the analytic solution the density field is transported without deformation. Numerical approximation procedures try to approximate this process of transport of the density field and due to approximation errors this transport is no longer deformation free. Such approximation errors tend to be more accurate when a structure is supported by many grid points x_i. The most simple grid is that of constant mesh length x_i+1 - x_i. Examples of such procedures are described in our book (see [1]). For this simple uniform grid the initial value and the numerically transported fields for different times are shown in fig 2 . The numerical method is described in detail in [1].

It is seen in fig 2 that the transport is rather accurate, though deformations and a loss of amplitude produce errors in the advection process. Such relatie accuracy of the transport process with many numerical processes is obtained with regular meshes x_i where x_i+1 - x_i is independent of i. Details are described in the MoW book (see [1]). This book describes some of the numerical methods in detail and describes also methods which maintain their accuracy when the grid becomes irregular. Such accuracy with irregular grids is dependent on parameters w_i depending on i. The software to compute the w_i and programs to accurately compute deriatives and the transport process for arbitrarily irregular grids are given in the application part of this Web page.
Work in this application area requires some basic knowledge of the programming language Fortran and the operating system Unix/Linux. A login to an account on our server will be necessary. On The Unix/Linux side (after login) a program similar to the one from [1] will be given.
While the program in [1] requires a regular one dimensional grid the Unix/Linux login offers a program for arbitrarily irregular grids. Acurate results can be obtained for irregular grids. Investigating the results for different resolutions of the same solution can be done and we expect a convergence of at least third order.