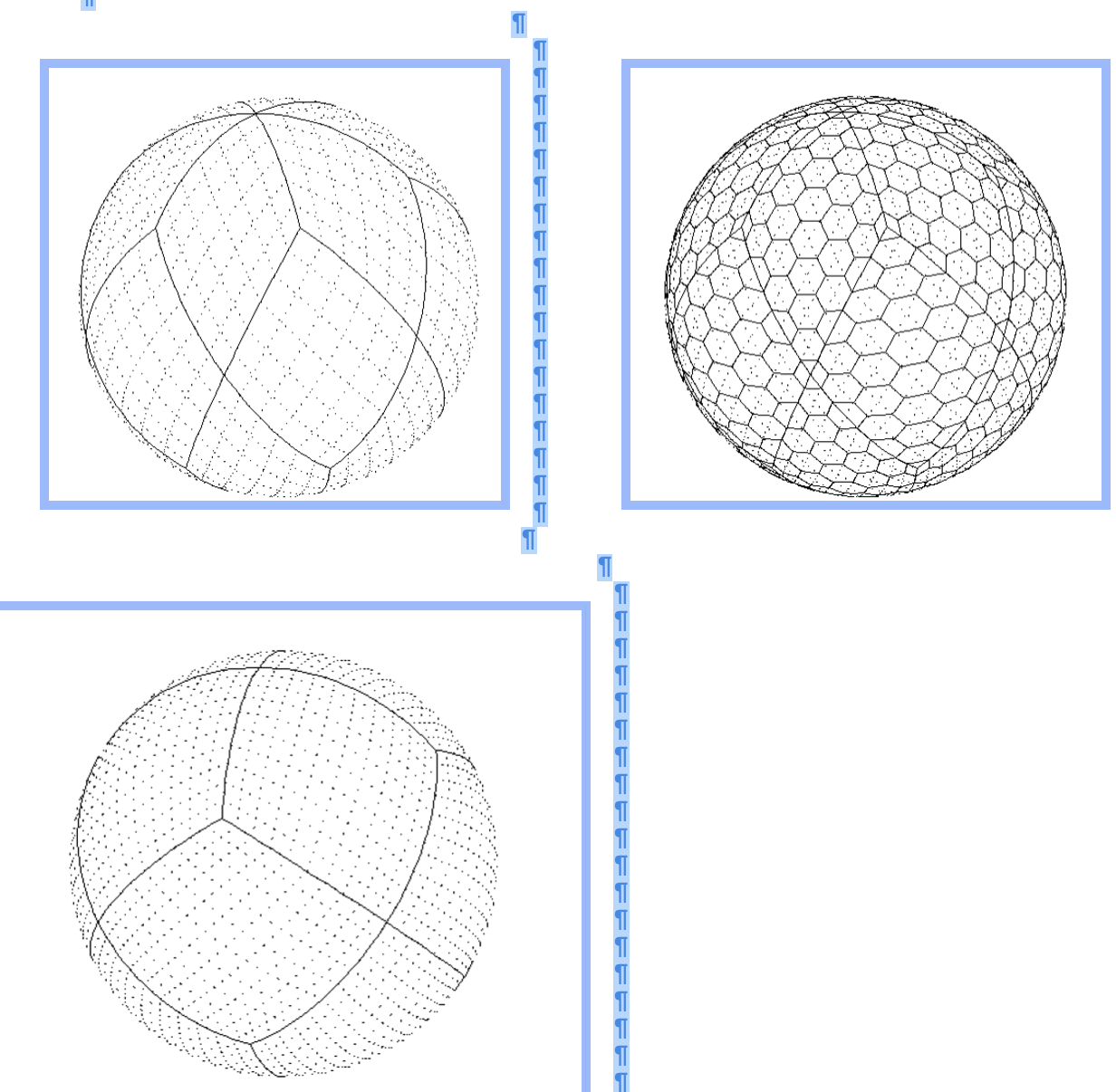
Grids on the sphere can be obtained by starting on a subdivision of the sphere into spherical quadrilaterals, popular choices are the icosahedron and the cubed sphere. Here also the T36 or R18 semi Platonic solid is used, which shows somewhat smaller rhomboidal areas than the other two choices and therefore the spherical grids generated are more homogeneous. Fig 1 shows a rhomboidal grid based on R18 and the hexagonal version obtained from this. The hexagons and rhomboids are not regular. Close to the boundaries of a basic area the rhomboids and hexagons are smaller. However, compared to similar diagrams for the cubed sphere and the icosahedron given in [1], the irregularity of the cells is smaller. To indicate the range of possibilities the R12 based rhomboidal grid is given at the bottom of fig 1.

Fig 1: a spherical rhomboidal grid based on the r18 solid (left). To the right a hexagonal version of this grid is shown. At the bottom the rhomboidal grid is shown for the R12 solid.
To show that small areas of the basic patches result into more regular grid, fig 2 gives the rhomboidal grid for the tetrahedral solid. This grid is sometimes called the YingYang grid. For this grid the difference between the longest and the smallest cell is large enough to be very evident in the figure.
The grid examples shown above have in common that the grid construction is given on rhomboidal patches which then are put together to form the grid on the sphere (see [1]).
The spheric part of this internet site gives tools (libraries, sample programs) to construct grids on the sphere and to form finite difference operations on such grids. To use these tools the interested reader must have basic knowledge of Unix/Linux and Fortran. The software can be used after a user login to an account on our server. For details see here.